Natural harmonics – Alternative touch points and how they are produced

Introduction to harmonics:
What are harmonics?

Natural string harmonics are sounds that are produced by slightly touching a string on specific places called nodes. In the case of the cello harmonics, which this article will focus on, they are very efficient, as the instrument’s range and the thickness of its strings allows a potent sound even in the highest harmonics.

 

What is a Natural Harmonic?

Let’s start with some knowledge of Acoustics. Through this, we can know all the tonal system and the harmonic progressions.

Every pitched sound we hear is a complex composite of many sub-set of sounds that are mathematically related to the main one, called “the fundamental note”. Each string has determined overtones that can produce. The related sounds or overtones are related to the “Overtone series” or also called the “Harmonic series”.

 

What is the Harmonic series?

The definition of the Harmonic series is the “sequence of sounds—pure tones, represented by sinusoidal waves—in which the frequency of each sound is an integer multiple of the fundamental, the lowest frequency.” Wikipedia. To see more go to this link.

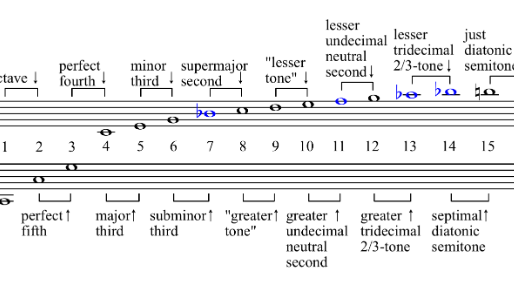
In lamen words, each string has multiple sounds related to the main or fundamental, and they are produced by the stimulation of certain areas or “nodes” on the string. Each string has the same mathematical relation, for example, the string of C (4th string on the cello) can produce the following natural harmonics:

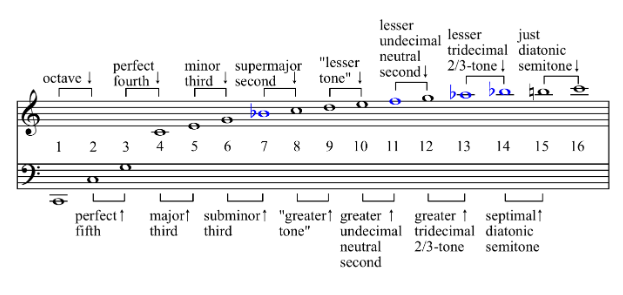
We can observe in this cello harmonics chart, from the first partial or fundamental note, C2, that the first harmonic has a relation to 2:1, that is to say, one octave higher.

The third harmonic is located a perfect fifth higher with a mathematical relation of 3:2; then the fourth harmonic, multiple of the second with a proportion of 4:1 gives us a double octave higher than the fundamental note—our 5th harmonic shows a major third (5:1 relation).

All the rest of the harmonics that are shown in the graphic above are definitively the most efficient for the production of natural harmonics are the ones explained here. Higher harmonics are multiple of these first five.

 

Notation of Natural Harmonics on the cello:

There are two ways of notating in classical music:

1.- A small circle over the note intended to sound as a harmonic

2.- A diamond-shaped note at the pitch where the node producing the desired note may be found on the string.

The notation varies according to the composer; many prefer the first method to leave the freedom of choice to the performer.

Examples of all possible nodes on the Cello

(From the book “The study of orchestration, 2nd edition”, page 49 (Samuel Adler).

Alternative Touch-points and How they are produced:

Natural harmonics are definitely a beautiful resource for every string player.

 

Cello harmonics:

Harmonics on cello are particularly useful, as the instrument has a powerful natural resonance so we can go very high up on the harmonic series; up to the 8th harmonic with almost no loss of the pitch or dynamic level.

On all string instruments, the harmonics are “mirrored”, that is to say, we have an equidistant distance from the middle of the string (7th position) for every harmonic to the nut and to the bridge. This means we can play the highest harmonics on the first position as well, and that is a powerful tool for the performer and also brings new possibilities for contemporary composers.

Here is a chart in which we can see the distance between harmonics:

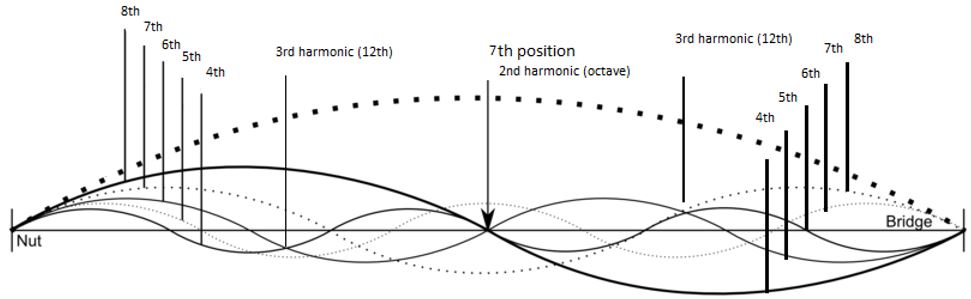
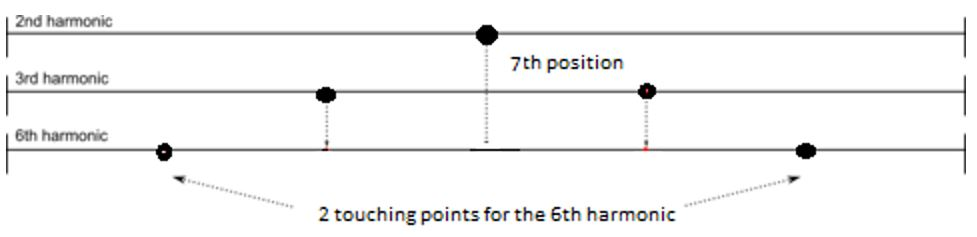
The graph above shows the relation among the nodes (where we produce the harmonics), the string (the line that lies from the nut to the bridge) and the sound waves showing how the string vibrates on both sides when we “activate” the nodes by slightly touching them.

 

Theory about Natural harmonics:

Natural harmonics are produced when we bow the string and touch a particular point on it with light finger pressure. The string vibrates on both sides of the touching finger as previously showed in the chart above.

The pitches generated to correspond to each partial of the open string; the first harmonic is called the fundamental (open string), the second harmonic is the octave, the third is the 12th (compound fifth), the fourth the double octave, etc.

Timbral Richness Vs. Overtones:

There is always a downside in all things: harmonics become overtone-weaker as they ascend through the harmonic series. The strongest and richest is the 2nd harmonic, the octave, which possess an amazing timbral resonance (played in the 7th position) but as we go high on the harmonic series, the overtones lose this resonant quality, so be careful when we replace the pressed note with the harmonic one; It is a very common mistake when we play or we compose music, as this can produce undesirable inconsistencies in the timbre when playing a melodic passage.

Alternative Touch-points:

How to play natural harmonics? Something very important when playing harmonics is to know that they can be produced at several of its nodal points, which means that we can play the same pitch in different parts throughout the fretboard.

Finding alternative touch points for a particular harmonic and knowing how many equivalent touch points are available will constitute a huge advantage for cellists and composer who want to deeply explore the timbrical possibilities of the instrument, as we can easily find the same pitch played with different strings, which will us various timbres for the same note, as well as cleverly composed fast passages without entangling difficult, if not impossible shifts for the left hand.

We will see a specific exercise for natural harmonics with change of position next time.